Unlocking Mathematical Precision: The Power of Mathematical Vocabulary.
In the realm of mathematics, where precision and accuracy reign supreme, the significance of a rich mathematical vocabulary cannot be overstated. It serves as the foundation upon which young minds build their understanding of numerical concepts, fostering a more nuanced and exact comprehension of mathematical operations. In this blog, we explore the importance of mathematical vocabulary and how it acts as a guiding force for children, enabling them to reason with greater clarity and accuracy.
1. Addition: Addend + Addend = Sum
The concept of addition is one of the first mathematical operations introduced to young learners. Understanding the terms involved - addend, addend, and sum - is crucial for precise reasoning.
Example: Imagine Sally has 3 apples, and her friend Tom gives her 4 more. The mathematical expression for this situation is 3 (addend) + 4 (addend) = 7 (sum). Knowing and using these terms helps children articulate their thought process clearly.
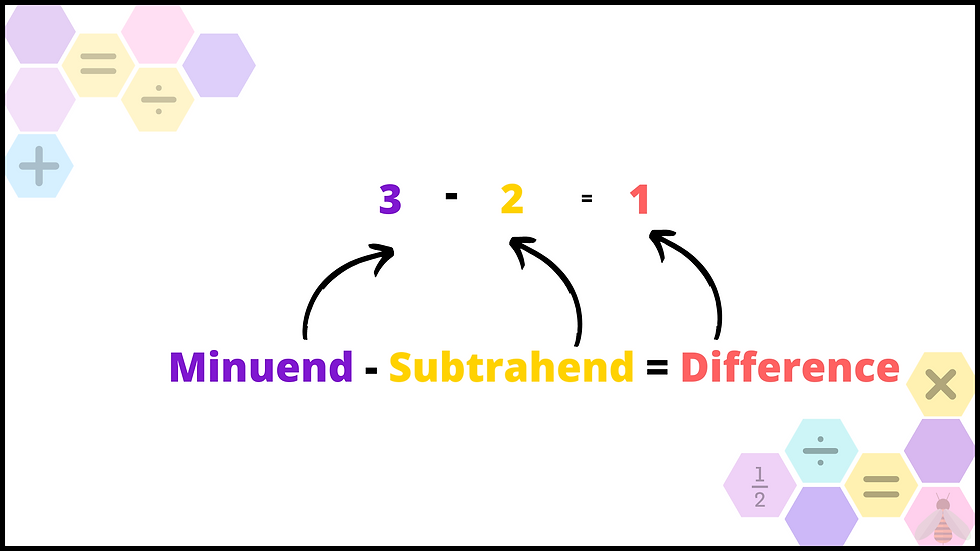
2. Subtraction: Minuend - Subtrahend = Difference
Subtraction is the reverse of addition, but it demands a distinct set of terms for clarity. The minuend is the starting quantity, the subtrahend is the amount to be taken away, and the difference is the result.
Example: Consider a scenario where Johnny has 8 candies, and he eats 3. The mathematical expression is 8 (minuend) - 3 (subtrahend) = 5 (difference). Using these terms helps children navigate through real-world situations with precision.
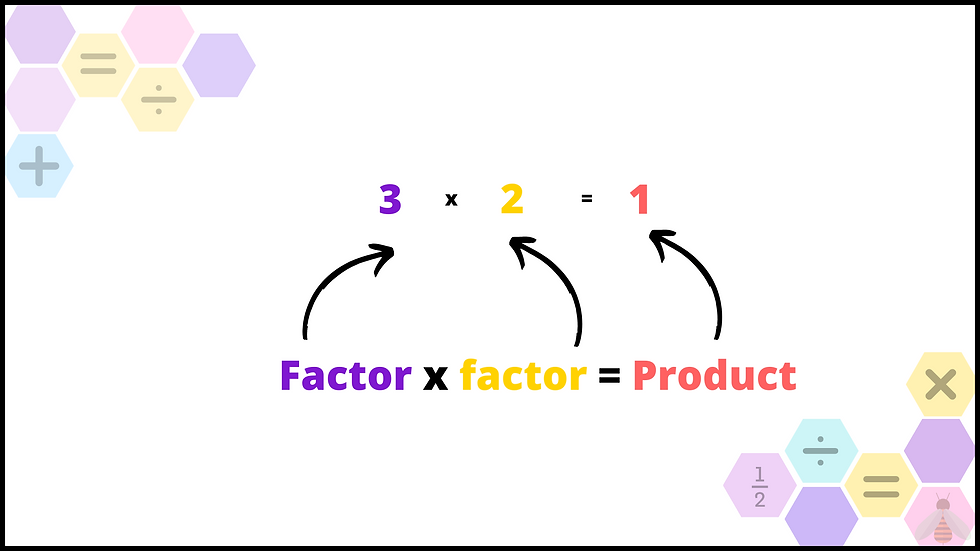
3. Multiplication: Factor x Factor = Product
As children progress in their mathematical journey, multiplication becomes a fundamental operation. Understanding the terms involved - factor, factor, and product - is essential for accurate reasoning.
Example: Suppose there are 4 bags, each containing 6 apples. The mathematical expression is 4 (factor) x 6 (factor) = 24 (product). Knowing these terms aids children in grasping the concept of repeated addition in a more structured manner.
4. Division: Dividend ÷ Divisor = Quotient
Division, the inverse of multiplication, introduces the terms dividend, divisor, and quotient. A solid grasp of these terms ensures precise communication of division processes.
Example: If there are 20 candies to be distributed among 4 friends, the mathematical expression is 20 (dividend) ÷ 4 (divisor) = 5 (quotient). Employing these terms helps children articulate the idea of sharing equally.
A robust mathematical vocabulary is the linchpin for children as they navigate the intricate world of numbers. By grasping and utilising terms like addend, sum, minuend, subtrahend, factor, product, dividend, divisor, and quotient, young learners not only enhance their mathematical fluency but also develop a more profound understanding of the processes involved. This linguistic precision lays the groundwork for a future where mathematical reasoning is second nature, paving the way for academic success and a lifelong love for mathematics.
You can download free posters to display in your classroom here.
Comments