Many number systems have developed across history and civilisations. We are probably most familiar with base 10. It is likely we count in base 10 because we have 10 fingers. We use digits 0 - 9 to count and use this with the decimal system too. There is a clear pattern and it seems intuitive to count in this way. The English language proves a degree of sophistication into number. 1, 2, 3... twenty-one, twenty-two, twenty-three... 11 and twelve are somewhat outcast and don't fit with the language structures of base 10, this is possibly due to the German etymology of such words.
Odds and evens.
Once children have mastered the number system and its patterns from a young age, it is time to begin to categorise the number system: this is usually done by introducing odd and even numbers.
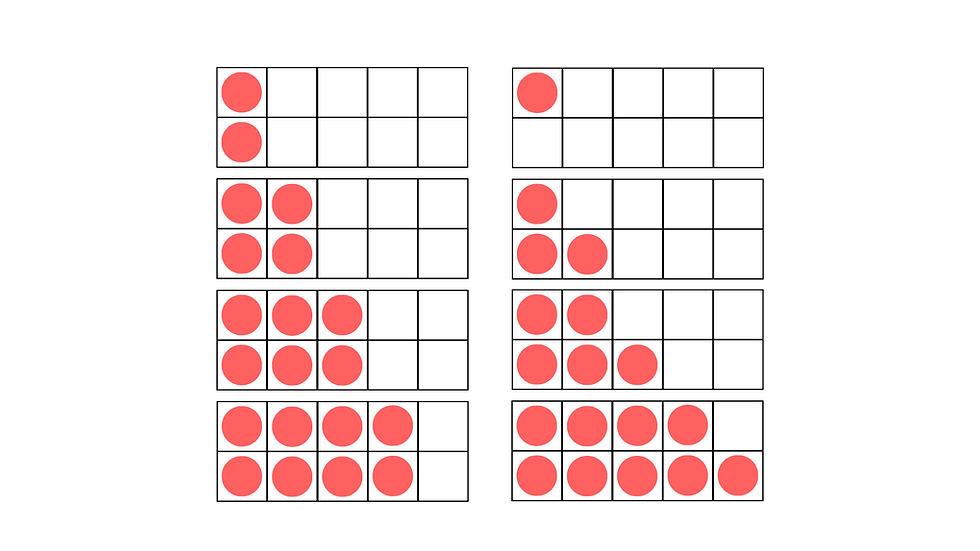
Introducing them using 10 frames can be useful to draw attention to the even ended properties of even numbers and the the uneven (odd) properties of odd numbers.
Once children have mastered this concept, they may generalise it to much larger numbers within the number system: this is often taught using 0, 2, 4, 6 8 are even and 1, 3, 5, 7 and 9 are odd. This stage should come after children explored representations using tens frames.
Why do two even numbers always equal an even number?
Now children may explore this concept to show that any two even numbers will always produce an even sum. The power of the representations allows children to generalise this clearly and effectively.
Why do two odd numbers always equal an even number?
Now, this time, it is clear two odd numbers always create an even sum.
Try asking children to explore why an odd number add an even number always gives an odd answer. The depth of understanding, vocabulary and mathematical thinking will be rich and deep.
What about multiplication with odd and even numbers?
Using the models of odd and even numbers, children may now explore the multiplicitative relationships between numbers. Exploring that an odd number multiplied by an even number multiplied by an even number will always give an even product or that an even number multiplied by an even number will always give an even product can be powerful ways to explore odd and even numbers.
The Chinese, do this in sophisticated ways to draw attention to the relation between odd and even numbers.
Fractions? Decimals?
Fractions defy the rules of categorisation with odds and evens and for good reason. Let's look at 3/5. One might consider this an odd number as it ends in a 5 (in fact both the numerator and denominator are odd numbers). However, when converted to a decimal this fractions becomes 0.6. This may be considered even and now we've got into a bit of a mathematical mess.
Similarly, with decimals we may consider 0.5 as an odd number due to the digit in the tenths fitting the idea of an off number ending in 5. But the problem is 0.5 is equivalent to 0.50 and now we might teach children that numbers which end in 0 are even. Again, another mathematical mess to avoid. We also explored earlier how Odd + Odd = Even but if we use the example 2.5 + 4.5 = 7 we can see this equals an odd number.
We must therefore differentiate that fractions and decimals are neither odd nor even. They're, well... fractions and decimals and operate outside of odd and even categorisations.
Categorisation.
We categorise our number system in many different ways. Odds and evens are just one way we might do this.
Natural numbers - positive whole numbers (sometimes called counting numbers). 1, 2, 3...
Integers - All whole numbers (including negative numbers and zero)
Rational numbers There are integers and fractions
Irrational numbers - Numbers which con not be expressed as fractions (such as pie)
Real numbers - Real numbers are all numbers except the imaginary or complex numbers.
Comments