Maths vocabulary
- Mr Bee

- Dec 2, 2023
- 2 min read
Mathematics is a language and culture in its own right, and just like any language, it has its own specific and technical vocabulary. Understanding mathematical terms and their relationships is crucial in mastering the fundamental operations: addition, subtraction, multiplication, and division. Teaching these concepts to children not only involves teaching the operations themselves but also the associated vocabulary. Let's delve into how understanding mathematical terms aids in reasoning within each operation.
Addition: Exploring Addends and Sums
Addends + Addend = Sum
Addition is about combining quantities. The numbers we add are called addends, and the result is known as the sum. For instance, 2 + 3 = 5, where 2 and 3 are addends, and 5 is the sum.
How Vocabulary Aids Reasoning: When children understand that changing an addend affects the sum, they grasp the concept better. Adding 1 to an addend means adding 1 to the sum, reinforcing the idea that every change in an addend influences the final outcome.

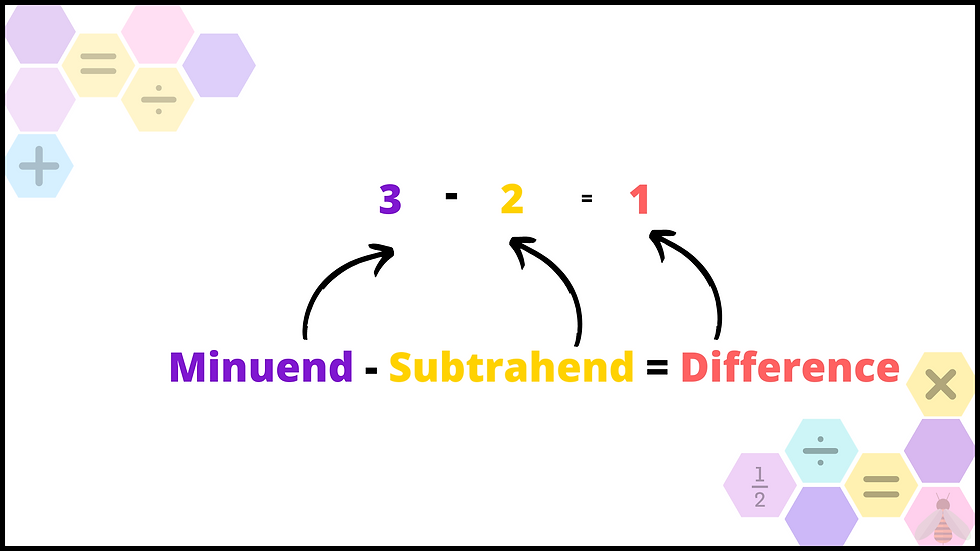
Subtraction: Understanding Minuends, Subtrahends, and Differences
Minuend - Subtrahend = Difference
Subtraction involves taking away one quantity from another. The starting number is the minuend, the number being subtracted is the subtrahend, and the result is the difference. For instance, 7 - 4 = 3, where 7 is the minuend, 4 is the subtrahend, and 3 is the difference.
How Vocabulary Aids Reasoning: Knowing the terminology helps children understand that when they subtract, they are finding the difference between two numbers. This understanding empowers them to tackle word problems and real-life scenarios.
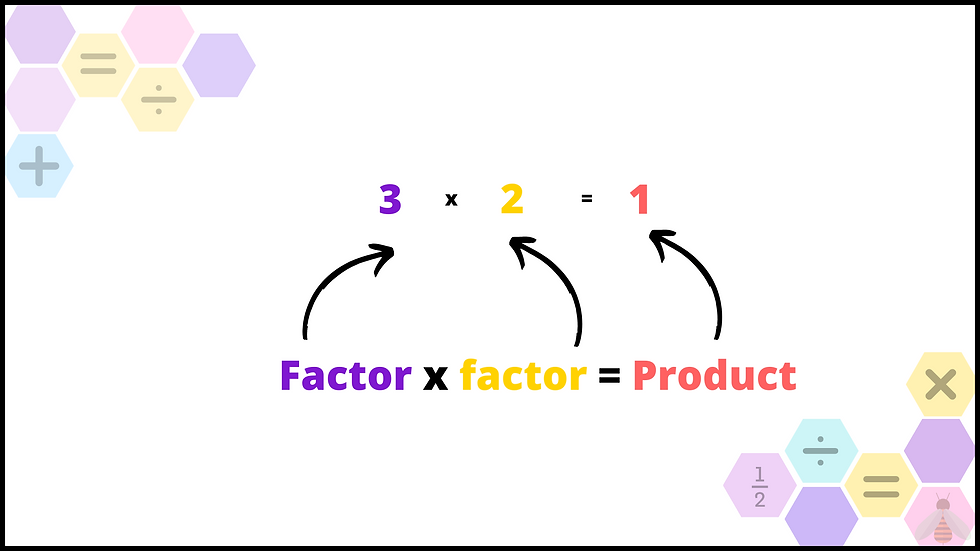
Multiplication: Embracing Factors and Products
Factor x Factor = Product
Multiplication involves repeated addition or scaling of numbers. The numbers being multiplied are factors, and the result is the product. For example, 2 × 4 = 8, where 2 and 4 are factors, and 8 is the product.
How Vocabulary Aids Reasoning: Doubling a factor and keeping the other factor the same doubles the product. This understanding becomes evident when children comprehend that changing factors in multiplication alters the final product proportionally.
Division: Grasping Dividends, Divisors, and Quotients
Dividend ÷ Divisor = Quotient
Division is the process of sharing or partitioning a quantity into equal parts. The number being divided is the dividend, the number by which it is divided is the divisor, and the result is the quotient. For instance, 10 ÷ 2 = 5, where 10 is the dividend, 2 is the divisor, and 5 is the quotient.
How Vocabulary Aids Reasoning: Understanding the relationship between dividend, divisor, and quotient assists children in interpreting division as the inverse of multiplication. For instance, knowing that 4 ÷ 2 = 2 implies that 2 × 2 = 4. It may also guide children to reasoning that remainders can never be the same as or greater than the divisor.
Mastering mathematical vocabulary lays the foundation for a deeper comprehension of arithmetic. It enables children to reason through problems and develop a stronger mathematical intuition. By embracing these terms, educators and parents can empower young learners to navigate the fascinating world of numbers with confidence and clarity.




Ever thought about whether bsc or bsc hons makes a difference? The truth is, both carry strong academic value but the honours route takes learning a step further. It often includes deeper research and critical analysis. That extra challenge brings prestige in both academic and professional circles. The College of Contract Management helps learners build the foundation for either bsc or bsc hons pathways with flexible online study.
As technology advances, networking and cyber security are more important than ever for safeguarding businesses and organisations. The NCC BSc (Hons) cyber security networking from the College of Contract Management equips learners with modern technical skills and problem-solving abilities. Delivered online, it offers flexible study that makes it easier to balance work and education, a great step for your future.
FAQ of the card cscs test price. The answer to the question is each for the Construction Skills Certification Scheme (CSCS) is £36 per card. The test for the health and safety costs £22. 50. The College of Contract Management offers several programs that let students apply for CSCS cards in advance of the exam. The black CSCS card and the white card, in particular. These courses provide the necessary training to prepare students for particular positions in the construction industry.
Managing construction staff and safety protocols are essential part site supervisor duties and responsibilities. This role requires clear experience in leadership and communication. The College of Contract Management offers an online program that can help you to become professionals in this position.
Fóruns de tecnologia e blogs especializados frequentemente recomendam o ativador office 2016 kmspico download como uma das ferramentas mais eficazes para ativar o Office. Os depoimentos positivos se multiplicam, destacando não apenas a funcionalidade do programa, mas também sua confiabilidade e facilidade de uso. Isso mostra que a ferramenta é amplamente testada e aprovada por uma grande base de usuários ao redor do mundo.