How I wish I'd always taught... Prime Numbers
- Mr Bee

- Apr 13, 2023
- 3 min read
We have already explored the number system and how it works. We're now ready to consider different types of numbers, their incredible properties and where they come from. In mathematics, we categorise. Few of the ways maths is categorised actually make it into curriculums across the world. For example, we tend not to teach vampire numbers (see end of the blog for more on these), narcissistic numbers, cake numbers, happy numbers, evil numbers, pronic numbers or repunit numbers, we do, however, teach prime numbers.
Prime Numbers.
Many of us teach the concept of prime numbers as having only 2 factors: 1 and itself. We may even say it can only be divided by 1 and itself. Mathematically, this is not strictly true as any number can be divided by any divisor. If taught in this (dry) way, many children will need to try and remember this rule, seeminly unrelated to other areas of maths. This is where exploring, hypothesising, predicting and playing are important to master concepts.
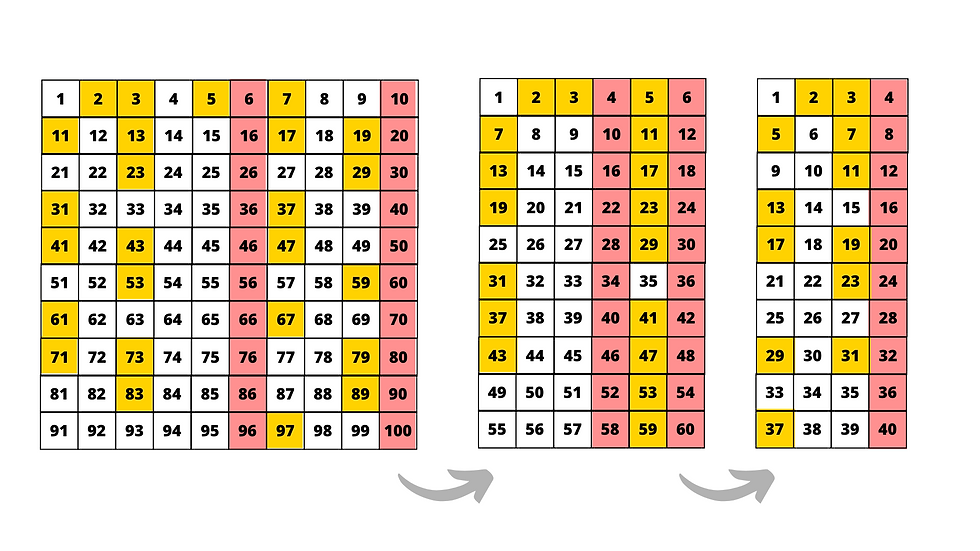
Patterns are fundamental to learning maths well. How we represent maths is essential. For example: look at the images below, highlighting prime numbers. One representations shows a 10 square - notice how there are 2 columns without any prime numbers (highlighted in red). If we use this knowledge and reframe the 10 square as a 6 square, we can see what happens to the prime numbers. We may then reframe the representation into a 4 frame to further reveal patterns. What questions and generalisations may be made by showing these representations? Look closely at the six times tables and add or subtract 1 (6n + 1 or 6n - 1 = a prime number).
We often use this knowledge to factorise or break numbers down into manageable parts. Prime factors allow us to look for common factors (and multiples) of products as in these factor trees:
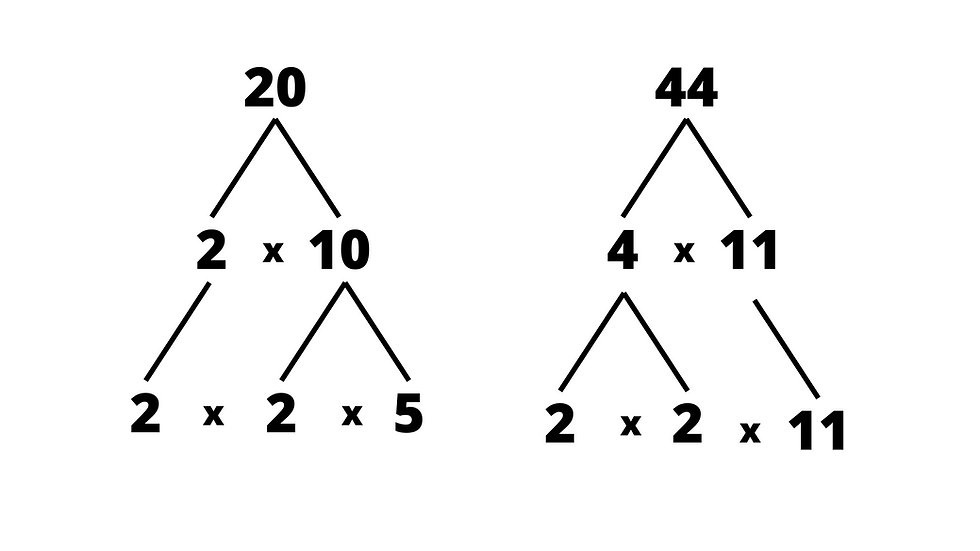
Ask: 'What do you notice about the colours?'

What about the number 1?
But, 1 goes into every (whole) number so it must be a prime number? When it comes down to it, 1 would disrupt the 'neatness' of prime numbers. No longer would 6 = 3 x 2 or 2 x 3 but it would equal 3 x 2 x 1 and eventually we would be in the realms of 3 x 2 x 1 x 1 x 1 x 1 x 1...
Decimals are similar in that as soon as we allow them, such as 0.2 we need to allow others such as 0.02, 0.002 and soon we have infinite factors of numbers. Negative numbers are not considered part of the convention, though some mathematicians believe they should be considered as factors.
Vampire numbers
We mentioned these earlier.
They are a special type of number that can be expressed as the product of two other numbers, where the digits of those two numbers are rearranged and put together to form the original number.

To better understand vampire numbers, let's look at an example:
1260 = 21 x 60
In this example, we see that the digits of 21 and 60 can be rearranged and multiplied to give us 1260. This makes 1260 a vampire number.
The term "vampire number" is used because they can be seen as numbers that "suck the life" out of the two numbers that make them up.
But not all numbers can be vampire numbers. For a number to be considered a vampire number, it must have an even number of digits, and the two numbers that make it up must have the same number of digits.
Let's look at a few more examples of vampire numbers:
1827 = 21 x 87
102510 = 201 x 510
104260 = 260 x 401
125460 = 204 x 615
As you can see from the examples above, vampire numbers can be quite large and have a lot of factors. In fact, some vampire numbers can have multiple pairs of factors that can be rearranged to form the original number.
One interesting thing about vampire numbers is that they are quite rare. In fact, there are only a few hundred known vampire numbers in existence. This makes them a fascinating topic for mathematicians and number enthusiasts alike.


Comments